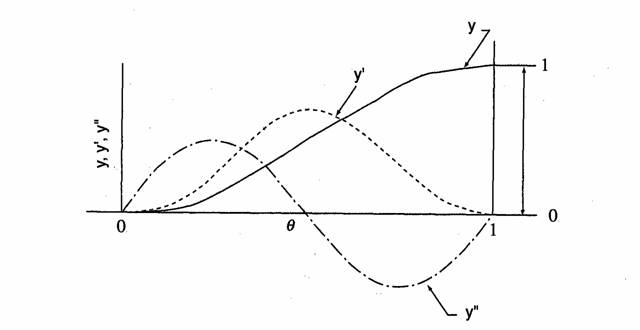
Leggi di moto
Le leggi di moto sono rappresentate nella forma y = f(q) , dove
| q |
è l’angolo adimensionale, va da 0 a 1 |
| y |
è l’alzata adimensionale, va da 0 a 1 |
| y’ = dy / dq |
è la velocità adimensionale |
| y’’ = d2y / dq 2 |
è l’accelerazione adimensionale |
Per calcolare i punti del profilo primitivo di un tratto di camma, con una rotazione da β0 a β1 e alzata totale H, si procede in questo modo:
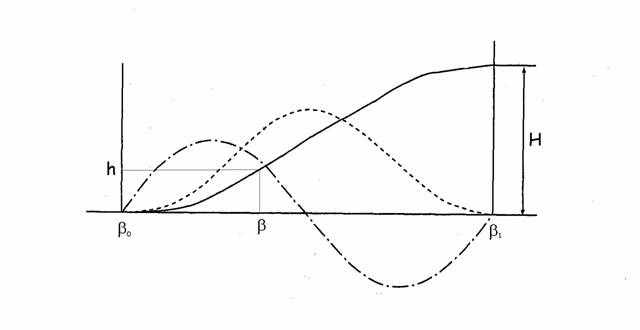
1. Per ogni angolo b si calcola l’angolo adimensionale q
q = (b - b0) / (b1 - b0)
2. Noto q, si calcola l’alzata adimensionale y = f(q) con la formula della legge di moto (es. cicloide)
y = 1 / p (p q - 0.5 sin (2 p q))
3. Infine si calcola l’alzata effettiva h
h = H y
Velocità costante
y = q
y’ = 1
y” = 0
Accelerazione costante
per q < 0.5
y = 2 q 2
y’ = 4 q
y” = 4
per q ³ 0.5
y = 1 – 2 (1 - q) 2
y’ = 4 (1 - q)
y” = -4
Parabola in salita (quadratic spline)
y = q 2
y’ = 2 q
y” = 2
Parabola in discesa (quadratic spline)
y = 1 – (1 - q) 2
y’ = 2 (1 - q)
y” = -2
Cicloide (cycloidal, sine-squared velocity)
y = 1 / p (pq - ½ sin (2 p q))
y’ = (1 - cos (2 p q))
y” = 2 p · sin (2 p q)
Armonica (simple harmonic)
y = ½ (1 - cos (p q))
y’ = ½ p sin (p q)
y” = ½ p 2 cos (p q)
Ellittica (0<a<1)
a = rapporto fra gli assi dell'ellisse
y = ½ (1 - (cos (p q)) / (Ö(1 - (a 2 - 1) / a 2 (sin (p q)) 2)))
y’ = 0.5 p a sin (q p) / ((1 - a 2) sin (q p) 2 + a 2) 1 . 5
y” = 0.5 p 2 a cos (q p) (2 (a 2 - 1) sin (q p) 2 + a 2) / ((1 - a 2) sin (q p) 2 + a 2) 2 . 5
Doppia cicloide
per q < a
y = 2 a 1 / p (p q / 2 / a - 0.5 sin (2 p q / 2 / a))
y’ = (1 - cos (p q / a))
y” = 1 / a p sin (p q / a)
per q ³ a
y = - (1 - 2 a) 1 + 2 (1 - a) 1 / p (p ((q - a) / 2 / (1 - a) + ½) - ½ sin (2 p ((q - a) / 2 / (1 - a) + ½)))
y’ = (1 - cos (2 p ((q - a) / 2 / (1 - a) + ½)))
y” = 1 / (1 - a) p sin (2 p * ((q - a) / 2 / (1 - a) + ½))
Cicloide + Armonica
per q < a
y = 2 a 1 / p (p q / 2 / a - ½ sin (2 p q / 2 / a))
y¢ = (1 - cos (p q / a)) '
y² = 1 / a p sin (p q / a)
per q ³ a
y = - (1 - 2 a) 1 + 2 (1 - a) 1 / p (p ((q - a) / 2 / (1 - a) + ½) - ½ sin (2 p ((q - a) / 2 / (1 - a) + ½)))
y’ = (1 - cos (2 p ((q - a) / 2 / (1 - a) + ½)))
y” = 1 / (1 - a) p sin (2 p ((q - a) / 2 / (1 - a) + ½))
Biarmonica
y = ½ ((1 - cos (p q)) - 1 / 4 (1 - cos (2 p q)))
y’ = ½ (p sin (p q) - ½ p sin (2 p q))
y” = ½ (p 2 cos (p q) - p 2 cos (2 p q))
Biarmonica inversa
y = ½ ((1 - cos (p q)) + 1 / 4 (1 - cos (2 p q)))
y’ = ½ (p sin (p q) + ½ p sin (2 p q))
y” = ½ (p 2 cos (p q) + p 2 cos (2 p q))
Curve trigonometriche modificate
Trapezoidale generalizzata a 7 tratti
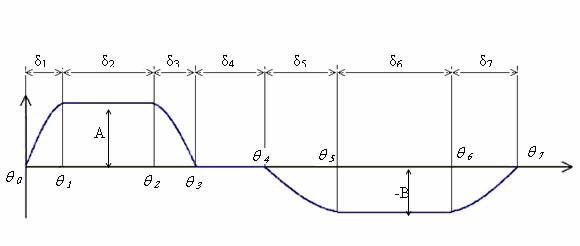
Accelerazione della legge trapezoidale a 7 tratti
q 0 = 0
q 1 = d1
q 2 = q 1 + d2
q 3 = q 2 + d3
q 4 = q 3 + d4
q 5 = q 4 + d5
q 6 = q 5 + d6
q 7 = 1
coefficienti necessari al calcolo
a11 = 2 d1 / p + d2 + 2 d3 / p
a12 = -2 d5 / p - d6 - 2 d7 / p
a21 = 2 d1 / p ((p - 2) / p d1 + d2 / 2) + (2 d1 / p + d2) (d2 / 2 + (p - 2) / p d3) + (2 d1 / p + d2 + 2 d3 / p) (2 d3 / p + d4 + 2 d5 / p)
a22 = (2 d7 / p + d6) ((p - 2) / p d5 + d6 / 2) + 2 d7 / p (d6 / 2 + (p - 2) / p d7)
A = -a12 / (a11 a22 - a12 a21)
B = a11 / (a11 a22 - a12 a21)
velocità nei 6 punti notevoli
V1 = 2 d1 / p A
V2 = a d2 + V1
V3 = 2 / p d3 A + V2
V4 = V3
V5 = V4 - B 2 d5 / p
V6 = V5 - B d6
alzate nei 6 punti notevoli
S1 = 2 (d12) / p A - (2 d1 / p)2 A
S2 = A / 2 d22 + V1 d2 + S1
S3 = (2 / p d3)2 A + V2 d3 + S2
S4 = S3 + A d4 (2 d1 / p + d2 + 2 d3 / p)
S5 = S4 + A d5 (2 d1 / p + d2 + 2 d3 / p) - B 2 d52 / p (1 - 2 / p)
S6 = S5 + V5 d6 - B d62 / 2
tratto I: 0 £ q £ q1
y = 2 d1 / p A (q - 2 d1 / p sin (p q / 2 / d1))
y’ = 2 d1 / p A (1 - cos (p q / (2 d1)))
y” = A sin (p q / (2 d1))
tratto II: q1 £ q £ q2
y = A / 2 (q - q1)2 + V1 (q - q1) + S1
y’ = A (q - q1) + V1
y” = A
tratto III: q2 £ q £ q3
y = (((2 / p d3)2) (A (1 - cos (p (q - q2) / 2 / d3))) + V2 (q - q2) + S2)
y’ = (2 / p d3 A sin (p (q - q2) / 2 / d3) + V2)
y” = (A cos (p (q - q2) / 2 / d3))
tratto IV: q3 £ q £ q4
y = V3 (q - q3) + S3
y’ = V3
y” = 0
tratto V: q4 £ q £ q5
y = -B 2 / p d5 (q - q4 - 2 / p d5 sin (p (q - q4) / 2 / d5)) + V4 (q - q4) + S4
y’ = -B 2 / p d5 (1 - cos (p (q - q4) / 2 / d5)) + V4
y” = -B sin (p (q - q4) / 2 / d5)
tratto VI: q5 £ q £ q6
y = (S5 + V5 (q - q5) - B (q - q5)2 / 2)
y’ = (V5 - B (q - q5))
y” = (-B)
tratto VII: q6 £ q £ 1
y = (((2 / p d7)2) B (cos (p (q - q6) / 2 / d7) - 1) + V6 (q - q6) + S6)
y’ = (V6 - B 2 / p d7 sin (p (q - q6) / 2 / d7))
y” = (-B cos (p (q - q6) / 2 / d7))
Casi particolari della Trapezoidale generalizzata a 7 tratti
Trapezoidale modificata
q 0 = 0
q 1 = 1 / 8
q 2 = 3 / 8
q 3 = 0.5
q 4 = q3
q 5 = 1 - q2
q 6 = 1 - q1
q 7 = 1
Sinusoidale modificata
q 0 = 0
q 1 = 1 / 8
q 2 = q 1
q 3 = 0.5
q 4 = q3
q 5 = 1 - q1
q 6 = q5
q 7 = 1
MCV50: velocità costante modificata (v è costante per il 50% del tratto)
q 0 = 0
q 1 = 1 / 16
q 2 = q 1
q 3 = 1 / 4
q 4 = 1 - q3
q 5 = 1 - q1
q 6 = q5
q 7 = 1
Curve polinomiali
Polinomiale 2-3
y = (3 q 2 - 2 q 3)
y’ = (6 q - 6 q 2)
y” = (6 - 12 q)
Polinomiale 3-4-5
y = (10 q 3 - 15 q 4 + 6 q 5)
y’ = (30 q 2 - 60 q 3 + 30 q 4)
y” = (60 q - 180 q 2 + 120 q 3)
Polinomiale 3-5
a = 0.1
per q < a
y = 178.76778 q 4 - 742.57426 q 5
y’ = 715.07112 q 3 - 3712.8713 q 4
y” = 2145.21336 q 2 - 14851.4852 q 3
per a £ q £ (1 - a)
y = -2.750275 (q - 0.5) 3 + 1.6639164 (q - 0.5) + 0.5
y’ = -8.250825 q 2 + 8.250825 q - 0.39878985
y” = 8.250825 - 16.50165 q
per q > (a-1)
y = 1 - (-742.57426 (1 - q) 5 + 178.76778 (1 - q) 4)
y’ = -3712.8713 q 4 + 14136.41408 q 3 - 20132.01443 q 2 + 12706.27184 q - 2997.80018
y” = -14851.4852 q 3 + 42409.24224 q 2 - 40264.02886 q + 12706.27184
Polinomiale 4-5-6-7
y = (35 q 4 - 84 q 5 + 70 q 6 - 20 q 7)
y’ = (140 q 3 - 420 q 4 + 420 q 5 - 140 q 6)
y” = (420 q 2 - 1680 q 3 + 2100 q 4 - 840 q 5)
Polinomiale 5-6-7-8-9
y = (126 q 5 - 420 q 6 + 540 q 7 - 315 q 8 + 70 q 9)
y’ = (630 q 8 - 2520 q 7 + 3780 q 6 - 2520 q 5 + 630 q 4)
y” = (5040 q 7 - 17640 q 6 + 22680 q 5 - 12600 q 4 + 2520 q 3)
Polinomiale 6-7-8-9-10-11
y = 462 q 6 - 1980 q 7 + 3465 q 8 - 3080 q 9 + 1386 q 1 0 - 252 q 1 1
y’ = -2772 q 1 0 + 13860 q 9 - 27720 q 8 + 27720 q 7 - 13860 q 6 + 2772 q 5
y” = -27720 q 9 + 124740 q 8 - 221760 q 7 + 194040 q 6 - 83160 q 5 + 13860 q 4
Polinomiale 8° grado
y = (6.09755 q 3 - 20.7804 q 5 + 26.73155 q 6 - 13.60965 q 7 + 2.56095 q 8)
y’ = (18.29265 q 2 - 103.902 q 4 + 160.3893 q 5 - 95.26755 q 6 + 20.4876 q 7)
y” = (36.5853 q - 415.608 q 3 + 801.9465 q 4 - 571.6053 q 5 + 143.4132 q 6)
Polinomiale 8° grado inversa
y = (2.63415 q 2 - 2.78055 q 5 - 3.1706 q 6 + 6.87795 q 7 - 2.56095 q 8)
y’ = (-20.4876 q 7 + 48.14565 q 6 - 19.0236 q 5 - 13.90275 q 4 + 5.2683 q)
y” = (-143.4132 q 6 + 288.8739 q 5 - 95.118 q 4 - 55.611 q 3 + 5.2683)
Polinomiale 11° grado
y = 0.336 q 5 - 1.89 q 6 + 4.74 q 7 - 6.615 q 8 + 5.32 q 9 - 2.31 q 1 0 + 0.42 q 1 1
y’ = 4.62 q 1 0 - 23.1 q 9 + 47.88 q 8 - 52.92 q 7 + 33.18 q 6 - 11.34 q 5 + 1.68 q 4
y” = 46.2 q 9 - 207.9 q 8 + 383.04 q 7 - 370.44 q 6 + 199.08 q 5 - 56.7 q 4 + 6.72 q 3
Polinomiale D (Berzak-Freudenstein)
y = 12.1 q 3 - 25.5 q 4 + 24.9 q 5 - 14.7 q 6 + 4.2 q 7
y’ = 29.4 q 6 - 88.2 q 5 + 124.5 q 4 - 102 q 3 + 36.3 q 2
y” = 176.4 q 5 - 441 q 4 + 498 q 3 - 306 q 2 + 72.6 q
Polinomiale E (Berzak-Freudenstein)
y = 5.35 q 3 + 8.2 q 4 - 35.74 q 5 + 32.46 q 6 - 9.27 q 7
y’ = -64.89 q 6 + 194.76 q 5 - 178.7 q 4 + 32.8 q 3 + 16.05 q 2
y” = -389.34 q 5 + 973.8 q 4 - 714.8 q 3 + 98.4 q 2 + 32.1 q
Armonica 1-3 di Gutman
y = q - 15 / 32 / p sin (2 p q) - 1 / 96 / p sin (6 p q)
y’ = 1 - 15 / 16 cos (2 p q) - 1 / 16 cos (6 p q)
y” = 15 p / 8 sin (2 p q) + 3 p / 8 sin (6 p q)
Armonica 1-3 di Freudenstein
y = q - ½ / p (27 / 28 sin (2 p q) + 1 / 84 sin (6 p q))
y’ = 1 - 27 / 28 cos (2 p q) - ½8 cos (6 p q)
y” = 2 p (27 / 28 sin (2 p q) + 3 / 28 cos (6 p q))
Armonica 1-3-5 di Freudenstein
y = q - 1125 / 1192 / 2 / p (sin (2 p q) + 1 / 54 sin (6 p q) + 1 / 1250 sin (10 p q))
y’ = 1 - 1125 / 1192 (cos (2 p q) + 1 / 18 cos (6 p q) + ½50 sin (10 p q))
y” = 2 p (1125 / 1192 (sin (2 p q) + 1 / 6 sin (6 p q) + 1 / 50 sin (10 p q)))
Armonica 1-3 di Weber
y = q - ½ / p (0.935454 sin (2 p q) + 0.02151533 sin (6 p q))
y’ = 1 - 0.06454598999 cos (6 q p) - 0.935454 cos (2 q p)
y” = 0.3872759399 p sin (6 q p) + 1.870908 p sin (2 q p)
Dudley 2-10-12-14
y = 1 / 64 (64 - 105 q 2 + 231 q 1 0 - 280 q 1 2 + 90 q 1 4
y’ = 3.28125 q (6 q 1 2 - 16 q 1 0 + 11 q 8 - 1)
y” = 3.28125 (78 q 1 2 - 176 q 1 0 + 99 q 8 - 1)
Peisekah 5-6-7-8-9
y = 126 q 5 - 420 q 6 + 540 q 7 - 315 q 8 + 70 q 9
y’ = 630 q 8 - 2520 q 7 + 3780 q 6 - 2520 q 5 + 630 q 4
y” = 5040 q 7 - 17640 q 6 + 22680 q 5 - 12600 q 4 + 2520 q 3
Peisekah 5-6-7-8-9-10-11
y = 336 q 5 - 1890 q 6 + 4740 q 7 - 6615 q 8 + 5320 q 9 - 2310 q 1 0 + 420 q 1 1
y’ = 4620 q 1 0 - 23100 q 9 + 47880 q 8 - 52920 q 7 + 33180 q 6 - 11340 q 5 + 1680 q 4
y” = 46200 q 9 - 207900 q 8 + 383040 q 7 - 370440 q 6 + 199080 q 5 - 56700 q 4 + 6720 q 3
Curve da funzioni algebriche polinomiali (7 tratti)
Curva universale a 7 tratti

Accelerazione della legge universale a 7 tratti
q 0 = 0
q 1 = d1
q 2 = q 1 + d2
q 3 = q 2 + d3
q 4 = q 3 + d4
q 5 = q 4 + d5
q 6 = q 5 + d6
q 7 = 1
velocità nei 6 punti notevoli
V1 = Am q1 2 (q1 2 - 4 q1 q1 + 6 q1 2) / (4 q1 3)
V2 = Am (q2 - q1) + V1
V3 = -Am / 4 / (q3 - q2) 3 (q3 - q2) 4 + Am (q3 - q2) + V2
V4 = V3
V5 = -Am / 4 / (q5 - q4) 3 (q5 - q4) 4 + Am / (q5 - q4) 2 (q5 - q4) 3 - 3 / 2 Am / (q5 - q4) (q5 - q4) 2 + V4
V6 = V5 - Am (q6 - q5)
alzate nei 6 punti notevoli
S1 = Am / (20 q1 3) ((q1 - q1) 5 + q1 5 - 5 q1 4 q1) + Am / 2 q1 2
S2 = Am / 2 (q2 - q1) 2 + V1 (q2 - q1) + S1
S3 = -Am / 20 / (q3 - q2) 3 (q3 - q2) 5 + Am / 2 (q3 - q2) 2 + V2 (q3 - q2) + S2
S4 = V3 (q4 - q3) + S3
S5 = -Am / 20 / (q5 - q4) 3 (q5 - q4) 5 + Am / 4 / (q5 - q4) 2 (q5 - q4) 4 - Am /2/ (q5 - q4)(q5 - q4) 3 + V4 (q5 - q4) + S4
S6 = S5 + V5 (q6 - q5) - Am (q6 - q5) 2 / 2
tratto I: 0 £ q £ q1
y = Am / (20 q1 3) ((q - q1) 5 + q1 5 - 5 q1 4 q) + Am / 2 q 2
y’ = Am q 2 (q 2 - 4 q q1 + 6 q1 2) / (4 q1 3)
y” = Am q (q 2 - 3 q q1 + 3 q1 2) / q1 3
tratto II: q1 £ q £ q2
y = Am / 2 (q - q1) 2 + V1 (q - q1) + S1
y’ = Am (q - q1) + V1
y” = Am
tratto III: q2 £ q £ q3
y = -Am / 20 / (q3 - q2) 3 (q - q2) 5 + Am / 2 (q - q2) 2 + V2 (q - q2) + S2
y’ = -Am / 4 / (q3 - q2) 3 (q - q2) 4 + Am (q - q2) + V2
y” = -Am / (q3 - q2) 3 (q - q2) 3 + Am
tratto IV: q3 £ q £ q4
y = V3 (q - q3) + S3
y’ = V3
y” = 0
tratto V: q4 £ q £ q5
y = -Am / 20 / (q5 - q4) 3 (q - q4) 5 + Am / 4 / (q5 - q4) 2 (q - q4) 4 - Am / 2 / (q5 - q4) (q - q4) 3 + V4 (q - q4) + S4
y’ = -Am / 4 / (q5 - q4) 3 (q - q4) 4 + Am / (q5 - q4) 2 (q - q4) 3 - 3 / 2 Am / (q5 - q4) (q - q4) 2 + V4
y” = -Am / (q5 - q4) 3 (q - q4) 3 + 3 Am / (q5 - q4) 2 (q - q4) 2 - 3 Am (q - q4) / (q5 - q4)
tratto VI: q5 £ q £ q6
y = S5 + V5 (q - q5) - Am / 2 (q - q5) 2
y’ = V5 - Am (q - q5)
y” = -Am
tratto VII: q6 £ q £ 1
y = Am (q - q6) 5 / (20 (1 - q6) 3) - Am / 2 (q - q6) 2 + V6 (q - q6) + S6
y’ = Am (q - q6) 4 / (4 (1 - q6) 3) - Am (q - q6) + V6
y” = Am (q - q6) 3 / (1 - q6) 3 - Am
Casi particolari della Curva universale a 7 tratti
SMT-3
q0 = 0
q1 = 1 / 8
q2 = 3 / 8
q3 = ½
q4 = q3
q5 = 1 - q2
q6 = 1 - q1
q7 = 1
S3 = 0.5
Am = 20 S3 / (9 q3 2 - q2 2 + q1 2 + 2 q2 q3 - 5 q1 q3)
SMS-3
q0 = 0
q1 = 1 / 8
q2 = 1 / 8
q3 = ½
q4 = q3
q5 = 1 - q2
q6 = 1 - q1
q7 = 1
S3 = 0.5
Am = 20 S3 / (9 q3 2 - 3 q1 q3)
SMCV-3
q0 = 0
q1 = 1 / 16
q2 = 1 / 16
q3 = 1 / 4
q4 = 1 - q3
q5 = 1 - q2
q6 = 1 - q1
q7 = 1
Am = 1 / (-3 / 5 q3 2 - 3 / 10 q1 q3 + 3 / 4 q3)
SHP-5
y = 28 q 3 - 48 q 3 . 5 + 21 q 4
y’ = 84 q 2 - 168 q 2 . 5 + 84 q 3
y” = 168 q - 420 q 1 . 5 + 252 q 2
SPLINE
Bezier:
I punti dati sono approssimati con un polinomio di Bernstein.
B-Spline:
Per alcuni valori particolari del numero di nodi della curva
approssimante si ottengono le seguenti curve:
|
2 |
segmenti di retta |
|
3 |
curve quadratiche |
|
n. punti da approssimare |
spline di Bezier |
C-Spline:
I punti dati sono interpolati da una spline cubica.
T-Spline:
I punti dati sono interpolati da una spline a tensione esponenziale.
Valori grandi della tensione appiattiscono la curva.